用高中数学解决求最小值问题（探索最优解决方案，提高解题技巧）

数学是一门重要的学科，广泛应用于各个领域。在高中数学中，求最小值是一个常见的问题。本文将介绍一些以高中数学为基础的方法，帮助读者更好地解决求最小值的问题，并提高解题技巧。

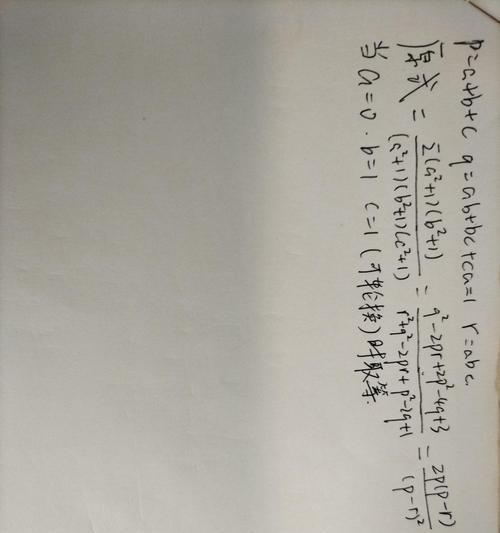
一、定义最小值概念及其应用

在数学中，最小值指的是给定中的最小元素。在实际问题中，我们常常需要找到某个函数或方程的最小值，以满足特定的条件或优化问题。通过对最小值的定义和应用的介绍，我们可以更好地理解求最小值的意义和用途。

二、使用导数法求函数的最小值

导数法是解决求函数最小值问题的常用方法之一。我们需要知道如何求函数的导数，并熟悉导数与函数的关系。通过求导等条件，我们可以找到函数的极小值点，并判断其是否为最小值。这一方法在解决一元函数最小值问题时尤为有效。

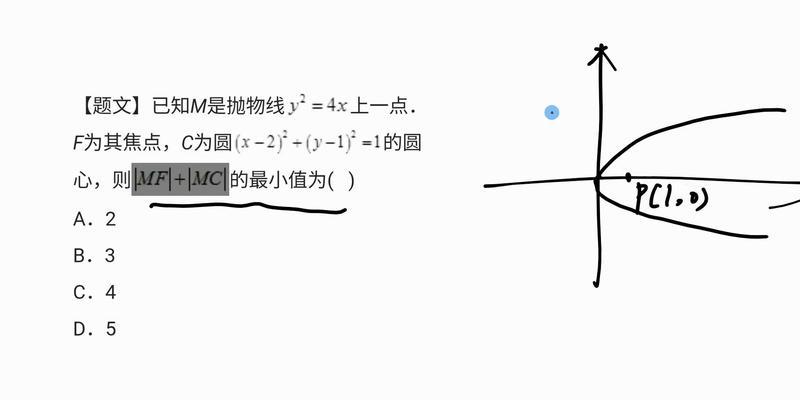
三、利用平方差和法求最小二乘法

最小二乘法是一种利用平方差和法求最小值的数学方法。它常用于拟合数据，寻找最佳拟合曲线或直线。通过最小二乘法，我们可以确定函数的系数，从而使得拟合曲线或直线与实际数据的误差最小。

四、应用拉格朗日乘数法求多元函数的最小值

拉格朗日乘数法是解决多元函数最小值问题的重要方法。通过引入拉格朗日乘子，我们可以将多元函数的最小值问题转化为带有约束条件的问题，进而求得最优解。这一方法在优化问题中广泛应用，例如经济学、工程学等领域。

五、使用二次函数图像法求最小值

二次函数图像法是一种直观且易于理解的方法，适用于解决求解最小值的问题。通过对二次函数的图像进行分析，我们可以确定函数的最小值点，并进一步推导出最小值。这一方法在高中数学中经常出现，并且适用于许多实际问题。

六、运用绝对值法求含有绝对值的最小值问题

绝对值法是一种解决含有绝对值的最小值问题的常见方法。通过对绝对值函数的性质和图像进行分析，我们可以确定函数的最小值点，并求得最小值。这一方法在解决绝对值函数相关问题时非常实用。

七、使用二分法求最小值

二分法是一种基于区间缩小的方法，可以帮助我们快速找到函数的最小值。通过不断地取区间中点，比较函数值，并根据结果缩小区间范围，我们可以逐步逼近最小值点，从而得到最小值。这一方法在数值计算和优化问题中具有广泛的应用。

八、利用数学模型求最优解

数学模型是将实际问题抽象化的工具，可以帮助我们求解最优解。通过建立数学模型，并运用相关的数学工具和技巧，我们可以求解函数或方程的最小值，并找到满足特定条件的最优解。这一方法在实际问题求解中具有重要的作用。

九、考虑约束条件对最小值的影响

在求解最小值的过程中，我们常常会面临一些约束条件。这些约束条件对于最小值的求解过程和结果都会产生一定的影响。我们需要仔细考虑约束条件，并相应地调整解题思路和方法，以获得准确的最小值。

十、探索最优解决方案的多样性

在求解最小值问题时，我们可以尝试不同的方法和思路，以获得最优的解决方案。不同的方法可能适用于不同类型的问题，因此我们需要灵活运用数学知识和技巧，发掘问题的多样性和可解性。

十一、注重解题过程中的推理和证明

在解决求最小值的问题过程中，推理和证明是不可或缺的步骤。通过合理的推理和严谨的证明，我们可以确保解题思路和方法的准确性，并得到可靠的最小值。我们应当注重推理和证明能力的培养。

十二、注意最小值问题中常见错误和陷阱

在求解最小值的过程中，常常会出现一些常见的错误和陷阱。例如，忽略了特殊情况、计算错误等。为了避免这些错误和陷阱，我们需要细心思考、反复验证，并培养良好的数学思维习惯。

十三、扩展思维拓宽数学应用领域

数学是一门富有创造力的学科，可以应用于各个领域。通过求解最小值问题，我们可以拓宽思维、扩大数学应用的领域。同时，这也是提高数学水平和解题能力的一种途径。

十四、综合运用数学知识解决实际问题

最小值问题常常涉及实际应用，例如优化调度、最优路径等。通过综合运用各种数学知识和技巧，我们可以解决实际问题，并得到最优解决方案。这一过程不仅锻炼了我们的数学能力，也提高了问题解决的能力。

十五、数学求最小值方法的综合运用与拓展

通过本文对高中数学求最小值的方法的介绍，我们可以看到数学在求解最小值问题中的重要作用。通过综合运用各种方法和思路，并将数学知识应用于实际问题中，我们可以提高解题能力、培养创新思维，并为数学应用领域的发展做出贡献。